
어때요, 혹시 "양자역학" 하면 머리부터 아파오는 분들 계신가요? 🙋♀️🙋♂️ 걱정 마세요! 오늘 드 브로이 파장과 양자 터널링의 신비로운 세계로 함께 떠나볼 거니까요! 😎 마치 숨겨진 던전 탐험하듯이 흥미진진할 거예요. 😉 양자역학, 알면 알수록 너무 재밌거든요! ✨ 자, 그럼 지금부터 양자역학 고수가 되는 마법의 주문을 외워볼까요? 🧙♀️ 렛츠기릿! 🤩
오늘 탐험할 양자 던전 핵심 정보 3가지!
- 드 브로이 파장이 양자 터널링에 미치는 놀라운 영향! 😮
- 불확정성 원리와 드 브로이 파장의 숨겨진 연결고리! 🔗
- 에너지 장벽을 뚫고 지나가는 투과 확률 계산법! 📈
드 브로이 파장, 대체 뭐길래? 🤔
드 브로이 파장은 입자가 파동처럼 행동한다는 개념이에요. 마치 우리가 바닷가에서 파도를 보듯이, 전자나 양성자 같은 작은 입자들도 파동의 성질을 가진다는 거죠! 🌊 드 브로이 형님(프랑스의 물리학자 루이 드 브로이)이 이 사실을 밝혀내고 노벨상까지 받았다니, 정말 대단하죠? 🏆 드 브로이 파장은 입자의 운동량(p)과 플랑크 상수(h)를 이용해서 계산할 수 있는데, 공식은 다음과 같아요.
λ = h / p
여기서 λ는 파장, h는 플랑크 상수, p는 운동량입니다. 이 공식만 기억하면 여러분도 이제 드 브로이 파장 전문가! 😉
양자 터널링, 벽을 뚫고 지나간다고? 🤯
양자 터널링은 입자가 고전역학적으로 넘을 수 없는 에너지 장벽을 뚫고 지나가는 현상을 말해요. 마치 영화 속 주인공이 벽을 통과하는 것처럼요! 👻 "에이, 말도 안 돼!"라고 생각할 수 있지만, 실제로 우리 주변에서 일어나는 현상이랍니다. 예를 들어, 태양 내부에서 핵융합 반응이 일어나는 것도 양자 터널링 덕분이에요! ☀️
불확정성 원리, 알쏭달쏭해? 😵💫
불확정성 원리는 입자의 위치와 운동량을 동시에 정확하게 알 수 없다는 원리예요. 마치 그림자처럼, 하나를 정확히 알려고 하면 다른 하나가 흐릿해지는 거죠. 👤 이 원리는 드 브로이 파장과도 밀접한 관련이 있는데, 입자의 위치가 좁아질수록 운동량의 불확실성이 커지고, 반대로 운동량을 정확히 알수록 위치의 불확실성이 커진답니다. 🤔
에너지 장벽, 얼마나 높고 넓어야 할까? 🧱

에너지 장벽은 입자가 넘어야 할 에너지의 높이를 말해요. 장벽이 높을수록, 그리고 넓을수록 입자가 터널링을 통해 통과하기 어려워지죠. 마치 높은 산을 넘는 것과 같아요. ⛰️ 하지만 양자역학의 세계에서는 불가능은 없답니다! 아무리 높은 장벽이라도, 입자는 확률적으로 통과할 수 있어요! 🍀
투과 확률, 얼마나 뚫고 지나갈까? 뚫어뻥! 🧻
투과 확률은 입자가 에너지 장벽을 통과할 확률을 말해요. 이 확률은 에너지 장벽의 높이와 폭, 그리고 입자의 운동량에 따라 달라진답니다. 투과 확률을 계산하는 공식은 복잡하지만, 걱정 마세요! 우리는 직관적으로 이해하면 돼요. 😉 에너지 장벽이 낮고 좁을수록, 그리고 입자의 운동량이 클수록 투과 확률은 높아진답니다! 🚀 마치 로켓처럼 슝! 💨
| 에너지 장벽 높이 | 에너지 장벽 폭 | 입자 운동량 | 투과 확률 |
|---|---|---|---|
| 높음 ↑ | 넓음 ↑ | 낮음 ↓ | 낮음 ↓ |
| 낮음 ↓ | 좁음 ↓ | 높음 ↑ | 높음 ↑ |
고전역학적 직관과의 충돌, 멘붕?! 🤯
양자 터널링은 고전역학적 직관과는 완전히 다른 현상이기 때문에, 처음 접하는 사람들은 멘붕에 빠질 수도 있어요. 😵 하지만 걱정 마세요! 양자역학은 원래 우리의 직관과는 어긋나는 부분이 많답니다. 마치 거울 나라의 앨리스처럼, 상상력을 발휘해서 양자 세계를 탐험해 보세요! 🪞
슈뢰딩거 방정식, 양자역학의 핵심 열쇠! 🔑
슈뢰딩거 방정식은 양자역학에서 입자의 상태 변화를 기술하는 가장 기본적인 방정식이에요. 이 방정식을 풀면 입자의 파동함수를 알 수 있고, 파동함수를 통해 입자의 위치, 운동량, 에너지 등 다양한 물리량을 계산할 수 있답니다. 마치 게임 속 캐릭터의 능력치를 분석하는 것처럼요! 🎮 슈뢰딩거 방정식은 양자역학의 핵심 열쇠라고 할 수 있어요! 🗝️
드 브로이 파장, 우리 생활에 숨어있다? 🔦
드 브로이 파장은 우리 눈에 보이지 않지만, 첨단 기술 속에 숨어 있답니다. 예를 들어, 전자 현미경은 드 브로이 파장을 이용하여 아주 작은 물체를 관찰할 수 있게 해줘요. 마치 슈퍼맨의 엑스레이 시력처럼요! 🦸♂️ 또한, 반도체 소자나 양자 컴퓨터 등 미래 기술에도 드 브로이 파장이 중요한 역할을 할 것으로 기대되고 있어요. 🌟
양자 터널링, 암 치료에도 쓰인다? 💊
양자 터널링은 암 치료에도 활용될 수 있다는 연구 결과가 나오고 있어요. 양자 터널링을 이용하여 암세포만 선택적으로 파괴하는 기술이 개발된다면, 암 치료의 새로운 지평을 열 수 있을 거예요. 마치 마법 지팡이처럼 암세포를 뿅! 하고 없애주는 거죠. ✨
불확정성 원리, 보안 기술에도 활용된다? 🔒
불확정성 원리는 양자 암호 기술에도 활용될 수 있어요. 양자 암호는 불확정성 원리에 기반하여 해킹이 불가능한 안전한 통신을 가능하게 해준답니다. 마치 절대 뚫을 수 없는 철통 보안 시스템처럼요! 🛡️
드 브로이 파장과 블랙홀, 무슨 관계? 🌌
드 브로이 파장은 블랙홀 연구에도 중요한 역할을 해요. 블랙홀 주변에서는 양자 효과가 매우 강하게 나타나는데, 드 브로이 파장을 이용하여 블랙홀의 특성을 연구할 수 있답니다. 마치 우주의 비밀을 푸는 열쇠처럼요! 🔑
양자역학, 영화 속 상상이 현실로? 🎬

양자역학은 영화 속 상상력을 현실로 만들어 줄 가능성이 있어요. 예를 들어, 양자 얽힘을 이용한 순간 이동 기술이나, 양자 컴퓨터를 이용한 초고속 연산 등 미래 기술은 우리의 삶을 완전히 바꿔놓을 수 있을 거예요. 마치 SF 영화 속 한 장면처럼요! 🚀
양자 얽힘, 쌍둥이처럼 신기해! 👯♀️
양자 얽힘은 두 입자가 서로 연결되어 있어서, 한 입자의 상태가 변하면 다른 입자의 상태도 즉각적으로 변하는 현상이에요. 마치 쌍둥이처럼 서로 연결된 느낌이죠! 👯♂️ 양자 얽힘은 양자 통신, 양자 컴퓨팅 등 다양한 분야에 활용될 수 있답니다. 🔗
양자 중첩, 동시에 여러 곳에 존재한다?! 🤯
양자 중첩은 입자가 여러 상태를 동시에 가질 수 있는 현상이에요. 마치 동전이 던져지기 전처럼 앞면과 뒷면이 동시에 존재하는 것과 같아요. 🪙 양자 중첩은 양자 컴퓨터의 핵심 원리로, 기존 컴퓨터로는 풀 수 없는 복잡한 문제를 해결할 수 있게 해준답니다. 💻
양자 컴퓨터, 슈퍼컴퓨터 뛰어넘는다? 🚀
양자 컴퓨터는 양자역학적 현상을 이용하여 기존 컴퓨터보다 훨씬 빠르게 연산할 수 있는 컴퓨터예요. 양자 컴퓨터는 신약 개발, 금융 분석, 인공지능 등 다양한 분야에서 혁신을 가져올 것으로 기대되고 있어요. 마치 미래에서 온 슈퍼컴퓨터처럼요! 🤖
양자 센서, 세상에 없던 정밀함을! 🔬
양자 센서는 양자역학적 효과를 이용하여 기존 센서보다 훨씬 정밀하게 측정할 수 있는 센서예요. 양자 센서는 의료, 환경, 국방 등 다양한 분야에서 활용될 수 있으며, 이전에는 상상할 수 없었던 정밀한 측정을 가능하게 해준답니다. 마치 초능력 센서처럼요! 👁️
양자 시뮬레이션, 복잡한 현상 예측한다! 🧪
양자 시뮬레이션은 양자역학적 원리를 이용하여 복잡한 물리 현상을 모의 실험하는 기술이에요. 양자 시뮬레이션은 신물질 개발, 화학 반응 예측, 우주 진화 연구 등 다양한 분야에서 활용될 수 있으며, 실험 없이도 복잡한 현상을 예측할 수 있게 해준답니다. 마치 미래를 보는 수정구슬처럼요! 🔮
드 브로이 파장 글을 마치며… 📝
자, 어떠셨나요? 드 브로이 파장과 양자 터널링의 세계, 생각보다 흥미진진하지 않나요? 😉 양자역학은 어렵다고 생각하지 말고, 마치 퍼즐을 풀듯이 하나씩 알아가면 정말 재미있답니다. 🧩 오늘 배운 드 브로이 파장과 양자 터널링은 양자역학의 아주 작은 부분일 뿐이에요. 앞으로 더 많은 양자역학의 세계를 탐험하면서, 여러분도 양자 고수가 되기를 응원할게요! 🙌 혹시 궁금한 점이 있다면 언제든지 댓글로 물어봐 주세요! 🤗 그럼 다음에 또 만나요! 👋 뿅! 💫
드 브로이 파장 관련 동영상

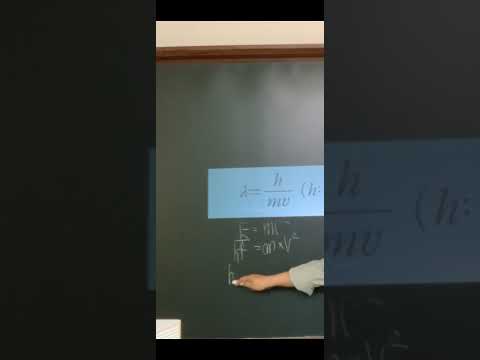






드 브로이 파장 관련 상품검색



