
어머나! 혹시 지금 양자역학 때문에 머리 싸매고 있나요? 🤯 보어의 원자 모형이 그렇게 만만치 않죠? 걱정 마세요! 오늘 제가 보어 모형을 정복하고, 심지어 나만의 계산기까지 만들 수 있는 비법을 알려드릴게요! 😎 이 글을 놓치면 후회할지도 몰라요! 😉
오늘 우리가 함께 알아볼 내용은요! 🚀
- 보어 모형의 핵심 공식 파헤치기: 에너지 준위와 파장을 계산하는 마법 같은 공식을 낱낱이 분석해 드립니다!
- 나만의 보어 모형 계산기 만들기: Python 또는 JavaScript를 사용해서 코딩 초보도 쉽게 따라 할 수 있는 계산기 제작 과정을 소개합니다!
- 수소 스펙트럼 예측하고 검증하기: 직접 만든 계산기로 수소 스펙트럼을 예측하고, 실제 데이터와 비교해서 정확도를 확인해 볼 거예요!
보어 모형, 대체 뭘까요? 🤔
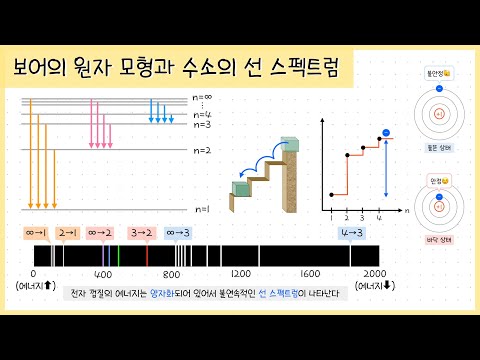
보어의 원자 모형은 20세기 초, 닐스 보어가 제시한 원자 구조 모형이에요. 러더퍼드의 행성 모형을 개선해서 전자가 특정한 에너지 준위에서만 존재할 수 있다는 가설을 제시했죠. 마치 태양 주위를 도는 행성처럼, 전자는 원자핵 주위를 특정한 궤도로 돌고 있다는 거예요. 💫
보어 모형의 핵심 공식, 정복하기! 🎯
보어 모형에서는 전자의 에너지 준위와 관련된 몇 가지 중요한 공식이 있어요. 이 공식들을 이해하면 보어 모형을 더 깊이 이해할 수 있답니다! 😉
에너지 준위 계산 공식 🧮
보어 모형에서 전자의 에너지 준위는 다음과 같은 공식으로 계산할 수 있어요.
$E_n = -frac{13.6 eV}{n^2}$
여기서 $E_n$은 n번째 에너지 준위, 그리고 n은 주양자수를 의미해요. 주양자수는 1, 2, 3과 같은 자연수 값을 가지며, 각 숫자는 전자가 존재할 수 있는 특정한 에너지 껍질을 나타냅니다. 껍질이 커질수록 (n이 커질수록) 에너지는 높아져요. 마치 계단을 올라가는 것처럼, 전자는 특정한 에너지 "계단"에만 존재할 수 있다는 거죠. 🪜
| 주양자수 (n) | 에너지 준위 (eV) |
|---|---|
| 1 | -13.6 |
| 2 | -3.4 |
| 3 | -1.51 |
| 4 | -0.85 |
| 5 | -0.54 |
파장 계산 공식 📏
전자가 에너지 준위 사이를 이동할 때, 에너지를 흡수하거나 방출하면서 빛을 내는데, 이때 방출되는 빛의 파장은 다음과 같은 공식으로 계산할 수 있어요.
$frac{1}{lambda} = R (frac{1}{n_1^2} – frac{1}{n_2^2})$
여기서 $lambda$는 파장, $R$은 리드베리 상수(약 $1.097 times 10^7 m^{-1}$), $n_1$과 $n_2$는 각각 전자가 이동하기 전과 이동한 후의 에너지 준위를 나타내요. 이 공식을 사용하면 전자가 어떤 에너지 준위 사이를 이동할 때 어떤 파장의 빛이 나오는지 예측할 수 있답니다. ✨
나만의 보어 모형 계산기 만들기! 💻

이제 이론은 충분히 공부했으니, 직접 코딩을 통해 보어 모형 계산기를 만들어 볼까요? Python이나 JavaScript와 같은 비교적 쉬운 프로그래밍 언어를 사용하면 간단하게 만들 수 있어요.
Python으로 계산기 만들기 🐍
import scipy.constants as const
# 리드베리 상수 (m^-1)
R = const.Rydberg
def calculate_wavelength(n1, n2):
"""파장 계산 함수"""
if n1 >= n2:
raise ValueError("n1은 n2보다 작아야 합니다.")
inverse_wavelength = R * (1/n1**2 - 1/n2**2)
wavelength = 1 / inverse_wavelength
return wavelength * 1e9 # 나노미터 단위로 변환
# 예시: n=2에서 n=3으로 전이할 때 파장 계산
try:
wavelength = calculate_wavelength(2, 3)
print(f"파장: {wavelength:.2f} nm")
except ValueError as e:
print(e)
JavaScript로 계산기 만들기 ☕

const R = 1.097e7; // 리드베리 상수 (m^-1)
function calculateWavelength(n1, n2) {
if (n1 >= n2) {
throw new Error("n1은 n2보다 작아야 합니다.");
}
const inverseWavelength = R * (1 / Math.pow(n1, 2) - 1 / Math.pow(n2, 2));
const wavelength = 1 / inverseWavelength;
return wavelength * 1e9; // 나노미터 단위로 변환
}
// 예시: n=2에서 n=3으로 전이할 때 파장 계산
try {
const wavelength = calculateWavelength(2, 3);
console.log(`파장: ${wavelength.toFixed(2)} nm`);
} catch (e) {
console.error(e.message);
}
수소 스펙트럼 예측하고 검증하기! 🧪
직접 만든 계산기를 사용해서 수소 스펙트럼을 예측하고, 실제 데이터와 비교해 볼까요? 수소는 가장 간단한 원자이기 때문에 보어 모형으로 비교적 정확하게 예측할 수 있어요.
라이먼 계열 (Lyman series) 🌠
라이먼 계열은 전자가 n=1로 떨어질 때 방출되는 빛의 스펙트럼을 말해요. 이 계열은 자외선 영역에 속하며, 다음과 같은 파장들을 가지고 있어요.
| 전이 (n → 1) | 파장 (nm) |
|---|---|
| 2 → 1 | 121.5 |
| 3 → 1 | 102.5 |
| 4 → 1 | 97.2 |
| 5 → 1 | 94.9 |
발머 계열 (Balmer series) 🌟
발머 계열은 전자가 n=2로 떨어질 때 방출되는 빛의 스펙트럼을 말해요. 이 계열은 가시광선 영역에 속하며, 다음과 같은 파장들을 가지고 있어요.
| 전이 (n → 2) | 파장 (nm) | 색깔 |
|---|---|---|
| 3 → 2 | 656.3 | 빨간색 |
| 4 → 2 | 486.1 | 파란색 |
| 5 → 2 | 434.0 | 남색 |
| 6 → 2 | 410.2 | 보라색 |
직접 만든 계산기를 사용해서 이 파장들을 계산해보고, 실제 스펙트럼 데이터와 비교해 보세요! 놀랍도록 일치하는 것을 확인할 수 있을 거예요! 🎉
보어 모형의 한계 🚧
보어 모형은 수소 원자의 스펙트럼을 비교적 정확하게 예측하지만, 몇 가지 중요한 한계를 가지고 있어요.
- 다전자 원자: 보어 모형은 전자가 두 개 이상인 원자에는 적용하기 어려워요. 전자 사이의 상호작용을 고려해야 하기 때문이죠.
- 스펙트럼 선의 세기: 보어 모형은 스펙트럼 선의 세기를 설명하지 못해요. 실제로 스펙트럼 선은 굵기가 다르고, 어떤 선은 더 밝게 빛나는데, 보어 모형으로는 이를 설명할 수 없답니다.
- 불확정성 원리: 보어 모형은 전자의 위치와 운동량을 동시에 정확하게 알 수 있다고 가정하지만, 이는 불확정성 원리에 위배돼요.
더 깊이 알아보기! 📚
보어 모형을 넘어서 더 복잡한 원자 모델을 탐구하고 싶다면, 다음과 같은 주제들을 공부해보는 것을 추천해요!
- 슈뢰딩거 방정식: 전자의 파동성을 고려한 슈뢰딩거 방정식을 배우면 원자를 더욱 정확하게 묘사할 수 있어요.
- 오비탈: 전자가 원자핵 주위에 존재할 확률 분포를 나타내는 오비탈 개념을 이해하면 원자의 화학적 성질을 더 잘 설명할 수 있답니다.
- 분광학: 빛과 물질의 상호작용을 연구하는 분광학을 배우면 다양한 원소와 분자의 스펙트럼을 분석하고, 그들의 구조와 성질을 파악할 수 있어요.
흥미로운 사례들! ✨
루비 레이저 💎
루비 레이저는 루비 결정에 빛을 쪼여서 특정한 파장의 빛을 증폭시키는 장치예요. 루비 결정 속의 크롬 이온은 특정한 에너지 준위를 가지고 있는데, 이 에너지 준위 사이의 전이 과정에서 특정한 파장의 빛이 방출된답니다. 보어 모형을 응용하면 루비 레이저의 작동 원리를 이해하는 데 도움이 될 거예요!
형광등 💡
형광등은 유리관 속에 수은 증기와 아르곤 가스를 넣고, 전기를 흘려보내 자외선을 발생시키는 원리로 작동해요. 이 자외선이 유리관 내부에 칠해진 형광 물질과 반응하여 가시광선을 내는 것이죠. 수은 원자의 에너지 준위와 전이 과정을 이해하면 형광등의 발광 원리를 더 깊이 이해할 수 있어요!
컨텐츠 연장 🚀
보어 모형의 역사적 배경 📜
보어 모형은 20세기 초, 물리학계에 큰 파장을 일으켰어요. 당시 러더퍼드의 원자 모형은 전자가 원자핵 주위를 돌면서 에너지를 잃고 결국 원자핵으로 붕괴한다는 문제점을 안고 있었죠. 보어는 플랑크의 양자 가설을 도입하여 전자가 특정한 에너지 준위에서만 존재할 수 있다는 혁신적인 아이디어를 제시했어요. 이 아이디어는 양자역학 발전의 중요한 발판이 되었답니다.
보어 모형과 현대 양자역학의 관계 ⚛️
보어 모형은 현대 양자역학의 초기 모델로서 중요한 의미를 가지지만, 몇 가지 근본적인 차이점이 있어요. 보어 모형은 전자의 궤도를 명확하게 정의하지만, 현대 양자역학에서는 전자의 위치와 운동량을 동시에 정확하게 알 수 없다는 불확정성 원리를 따르죠. 또한, 보어 모형은 전자의 파동성을 고려하지 않지만, 현대 양자역학에서는 전자를 파동 함수로 묘사한답니다.
다양한 원소의 스펙트럼 분석 🌈
보어 모형은 수소 원자에 대해서만 비교적 정확한 예측을 제공하지만, 다른 원소들의 스펙트럼은 훨씬 복잡한 양상을 보여요. 이는 전자 사이의 상호작용, 스핀-궤도 결합 등 다양한 요인들이 작용하기 때문이죠. 분광학 기술을 활용하면 다양한 원소들의 스펙트럼을 분석하고, 그들의 에너지 준위와 전자 구조를 파악할 수 있답니다.
분광학의 다양한 응용 분야 🔬
분광학은 다양한 분야에서 활용되고 있어요. 천문학에서는 별빛의 스펙트럼을 분석하여 별의 온도, 화학 성분, 운동 속도 등을 알아낼 수 있고, 화학에서는 물질의 스펙트럼을 분석하여 분자의 구조와 성질을 파악할 수 있죠. 또한, 의학에서는 혈액이나 소변의 스펙트럼을 분석하여 질병을 진단하는 데 활용되기도 한답니다.
양자 컴퓨팅의 미래 💻
양자역학의 원리를 이용한 양자 컴퓨팅은 미래 컴퓨팅 기술의 핵심으로 주목받고 있어요. 양자 컴퓨터는 큐비트라는 양자 비트를 사용하여 기존 컴퓨터로는 풀기 어려운 복잡한 문제를 해결할 수 있을 것으로 기대됩니다. 양자 컴퓨팅 기술이 발전하면 신약 개발, 인공지능, 암호 해독 등 다양한 분야에서 혁신을 가져올 수 있을 거예요!
보어의 원자 모형 글을 마치며… 👋
자, 오늘 보어의 원자 모형에 대해 함께 알아보고, 직접 계산기까지 만들어봤는데 어떠셨나요? 😉 보어 모형은 완벽한 모델은 아니지만, 원자의 구조와 스펙트럼을 이해하는 데 중요한 첫걸음이라고 할 수 있어요. 이 글이 여러분의 양자역학 공부에 조금이나마 도움이 되었기를 바라면서, 다음에 더 재미있는 주제로 만나요! 🤗 궁금한 점이 있다면 언제든지 댓글로 물어보세요! 😉
보어의 원자 모형 관련 동영상






보어의 원자 모형 관련 상품검색



