
어머, 여러분! 혹시 양자컴퓨팅에 대해 들어보셨나요? 🚀 미래를 바꿀 기술이라는데, 뭔가 복잡하고 어렵게 느껴지시죠? 😥 하지만 걱정 마세요! 양자컴퓨팅의 핵심인 ‘양자 게이트’를 완벽하게 파헤쳐서 여러분도 양자 고수가 될 수 있도록 쉽고 재미있게 알려드릴게요! 😉 지금 바로 양자 게이트의 세계로 함께 떠나볼까요? 🤩 안 보면 후회할걸요?! 😎
✨핵심 요약✨
- 양자컴퓨팅의 기본 원리 (큐비트, 중첩, 얽힘) 완벽 이해!
- CNOT, Hadamard, Pauli 게이트 종류별 회로도 & 유니타리 행렬 표현 마스터!
- Qiskit, Cirq 활용 꿀팁 대방출! 오류 보정 & 고급 알고리즘 학습 연계까지!
양자컴퓨팅, 왜 중요할까요? 🤔
양자컴퓨팅은 기존 컴퓨터로는 풀기 어려웠던 복잡한 문제를 해결할 수 있는 차세대 기술이에요. 신약 개발, 금융 모델링, 인공지능 등 다양한 분야에서 혁신을 가져올 것으로 기대되죠. 😲 특히, 암호 해독 분야에서 엄청난 잠재력을 가지고 있어서 보안 전문가들의 관심도 뜨겁답니다! 🔥
큐비트: 양자컴퓨팅의 기본 단위 ⚛️

기존 컴퓨터는 비트(0 또는 1)를 사용하지만, 양자컴퓨터는 큐비트(Qubit)를 사용해요. 큐비트는 0과 1의 상태를 동시에 가질 수 있는 ‘중첩’이라는 신기한 성질을 가지고 있어요. 마치 동전이 앞면과 뒷면을 동시에 보여주는 것과 같죠! 🪙 이러한 중첩 덕분에 양자컴퓨터는 훨씬 더 많은 정보를 동시에 처리할 수 있답니다. 👍
또 다른 핵심 개념은 ‘얽힘’이에요. 얽힘은 두 개의 큐비트가 서로 연결되어 하나의 시스템처럼 행동하는 현상이에요. 마치 쌍둥이처럼 한 큐비트의 상태를 측정하면 다른 큐비트의 상태도 즉시 알 수 있게 되죠! 👯♀️ 얽힘은 양자컴퓨팅의 계산 속도를 엄청나게 빠르게 만들어주는 마법 같은 힘이랍니다. 🧙
양자 게이트란 무엇일까요? 🚪
양자 게이트는 큐비트의 상태를 변화시키는 연산이에요. 마치 논리 회로에서 AND, OR 게이트처럼 양자 회로에서 큐비트를 조작하는 역할을 하죠. 양자 게이트를 조합하면 복잡한 양자 알고리즘을 구현할 수 있답니다. 🧩 다양한 양자 게이트 종류를 알아두면 양자컴퓨팅의 가능성을 더 넓게 이해할 수 있어요.
필수 게이트 3총사: CNOT, Hadamard, Pauli 🥇
양자 게이트 종류는 정말 다양하지만, 그중에서도 가장 기본적이고 중요한 게이트 3총사를 소개할게요! CNOT 게이트, Hadamard 게이트, Pauli 게이트는 양자컴퓨팅의 기초를 다지는 데 필수적인 요소들이랍니다.
CNOT 게이트: 양자 회로의 연결고리 🔗
CNOT (Controlled-NOT) 게이트는 두 개의 큐비트를 사용하는 게이트예요. 하나의 큐비트(제어 큐비트)의 상태에 따라 다른 큐비트(대상 큐비트)의 상태를 반전시켜요. 마치 스위치처럼 작동하는 거죠! 💡 CNOT 게이트는 양자 얽힘을 만들거나 양자 정보를 전송하는 데 사용돼요.
| 제어 큐비트 | 대상 큐비트 (입력) | 대상 큐비트 (출력) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
CNOT 게이트의 회로도 표현은 다음과 같아요. 제어 큐비트는 ●로, 대상 큐비트는 ⊕로 표시하죠.

CNOT 게이트의 유니타리 행렬 표현은 다음과 같아요.
[[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 0, 1],
[0, 0, 1, 0]]Hadamard 게이트: 중첩 상태 만들기 마법 ✨
Hadamard 게이트는 큐비트를 중첩 상태로 만들어주는 마법 같은 게이트예요. 🪄 큐비트가 0 또는 1의 상태로 주어지면, Hadamard 게이트는 이를 0과 1의 중첩 상태로 변환시켜요. Hadamard 게이트는 양자 알고리즘에서 초기 상태를 설정하거나 양자 간섭을 일으키는 데 사용돼요.
| 입력 큐비트 | 출력 큐비트 |
|---|---|
| 0 | (0 + 1) / √2 |
| 1 | (0 – 1) / √2 |
Hadamard 게이트의 회로도 표현은 간단하게 H로 표시해요.

Hadamard 게이트의 유니타리 행렬 표현은 다음과 같아요.
[[1/√2, 1/√2],
[1/√2, -1/√2]]Pauli 게이트: 큐비트 상태 반전! 🔄
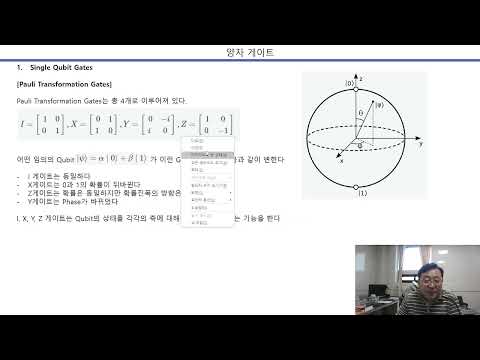
Pauli 게이트는 큐비트의 상태를 반전시키는 게이트예요. Pauli-X, Pauli-Y, Pauli-Z 세 가지 종류가 있어요.
- Pauli-X 게이트 (NOT 게이트): 큐비트의 상태를 0에서 1로, 1에서 0으로 반전시켜요. 기존 컴퓨터의 NOT 게이트와 같은 역할을 하죠. ❌
- Pauli-Y 게이트: 큐비트의 상태를 복소수 단위 i를 곱하여 반전시켜요. 🌀
- Pauli-Z 게이트: 큐비트의 위상을 반전시켜요. 💫
| 게이트 종류 | 입력 큐비트 | 출력 큐비트 |
|---|---|---|
| Pauli-X | 0 | 1 |
| Pauli-X | 1 | 0 |
| Pauli-Y | 0 | i1 |
| Pauli-Y | 1 | -i0 |
| Pauli-Z | 0 | 0 |
| Pauli-Z | 1 | -1 |
Pauli 게이트의 회로도 표현은 각각 X, Y, Z로 표시해요.

Pauli 게이트의 유니타리 행렬 표현은 다음과 같아요.
- Pauli-X:
[[0, 1], [1, 0]] - Pauli-Y:
[[0, -i], [i, 0]] - Pauli-Z:
[[1, 0], [0, -1]]
게이트 조합: 복잡한 연산 구현하기 🧮
양자 게이트를 여러 개 조합하면 더 복잡한 연산을 구현할 수 있어요. 예를 들어, CNOT 게이트와 Hadamard 게이트를 조합하면 양자 얽힘 상태를 만들 수 있죠. 🤩 다양한 게이트 조합을 통해 양자 컴퓨터의 잠재력을 최대한으로 끌어올릴 수 있답니다!
양자 회로 시뮬레이터 활용 꿀팁 💻
양자 회로를 직접 만들어보고 싶다면, 양자 회로 시뮬레이터를 활용해보세요! Qiskit (IBM)과 Cirq (Google)는 대표적인 양자 회로 시뮬레이터로, 파이썬 기반으로 사용하기 쉽고 다양한 기능을 제공해요. 🐍
Qiskit: IBM의 양자 컴퓨팅 플랫폼 🧊
Qiskit는 IBM에서 제공하는 오픈소스 양자 컴퓨팅 플랫폼이에요. Qiskit를 사용하면 양자 회로를 설계하고 시뮬레이션할 수 있을 뿐만 아니라, IBM의 실제 양자 컴퓨터를 사용하여 실험해볼 수도 있어요! 😮 Qiskit는 양자 알고리즘 개발, 양자 교육, 양자 연구 등 다양한 분야에서 활용되고 있답니다.
from qiskit import QuantumCircuit, transpile, Aer, execute
from qiskit.visualization import plot_histogram
# 양자 회로 생성
qc = QuantumCircuit(2, 2) # 2개의 큐비트와 2개의 고전 비트
qc.h(0) # 첫 번째 큐비트에 Hadamard 게이트 적용
qc.cx(0, 1) # CNOT 게이트 적용 (제어 큐비트: 0, 대상 큐비트: 1)
qc.measure([0, 1], [0, 1]) # 큐비트 측정 후 고전 비트에 저장
# 시뮬레이터 선택
simulator = Aer.get_backend('qasm_simulator')
# 회로 최적화
compiled_circuit = transpile(qc, simulator)
# 시뮬레이션 실행
job = execute(compiled_circuit, simulator, shots=1000)
result = job.result()
# 결과 분석
counts = result.get_counts(qc)
print(counts) # 측정 결과 출력
plot_histogram(counts) # 히스토그램으로 결과 시각화Cirq: Google의 양자 컴퓨팅 프레임워크 🌐
Cirq는 Google에서 제공하는 오픈소스 양자 컴퓨팅 프레임워크예요. Cirq는 양자 회로를 설계하고 시뮬레이션하는 데 사용되며, 특히 Google의 양자 컴퓨터를 활용하는 데 최적화되어 있어요. Cirq는 양자 알고리즘 개발, 양자 하드웨어 개발 등 다양한 분야에서 활용되고 있답니다.
import cirq
# 큐비트 생성
q0 = cirq.GridQubit(0, 0)
q1 = cirq.GridQubit(0, 1)
# 회로 생성
circuit = cirq.Circuit(
cirq.H(q0), # Hadamard 게이트 적용
cirq.CNOT(q0, q1), # CNOT 게이트 적용
cirq.measure(q0, key='q0'), # 큐비트 측정
cirq.measure(q1, key='q1') # 큐비트 측정
)
# 시뮬레이터 선택
simulator = cirq.Simulator()
# 시뮬레이션 실행
result = simulator.run(circuit, repetitions=1000)
# 결과 분석
print(result.histogram(key='q0')) # q0 측정 결과 출력
print(result.histogram(key='q1')) # q1 측정 결과 출력오류 보정: 양자컴퓨팅의 숙제 😥
양자컴퓨터는 외부 환경에 매우 민감해서 오류가 발생하기 쉽다는 단점이 있어요. 😭 양자 오류는 계산 결과에 큰 영향을 미칠 수 있기 때문에, 오류를 보정하는 기술이 매우 중요해요. 양자 오류 보정은 양자컴퓨팅의 실용화를 위한 핵심 과제랍니다. 💪
고급 양자 알고리즘 맛보기 🍬
양자 게이트를 이해했다면, 이제 고급 양자 알고리즘에 도전해볼 차례예요! 쇼어 알고리즘과 그로버 알고리즘은 양자컴퓨팅의 대표적인 알고리즘으로, 기존 컴퓨터로는 풀기 어려웠던 문제를 효율적으로 해결할 수 있어요.
쇼어 알고리즘: 암호 해독의 혁명 🔓
쇼어 알고리즘은 큰 수의 소인수 분해를 빠르게 수행하는 양자 알고리즘이에요. 쇼어 알고리즘이 실용화되면 현재 사용되는 RSA 암호 체계를 무력화할 수 있기 때문에 보안 분야에 큰 파장을 일으킬 수 있답니다. 💣
그로버 알고리즘: 데이터 검색의 달인 🔍
그로버 알고리즘은 정렬되지 않은 데이터베이스에서 특정 항목을 빠르게 검색하는 양자 알고리즘이에요. 그로버 알고리즘은 기존 컴퓨터 알고리즘보다 훨씬 빠르게 데이터를 검색할 수 있기 때문에 데이터 분석, 인공지능 등 다양한 분야에서 활용될 수 있답니다. 🚀
양자 게이트 종류: 후기와 관련 정보 📚
양자 게이트 종류를 공부하면서 양자컴퓨팅의 무한한 가능성을 엿볼 수 있었어요. 🤩 아직은 초기 단계이지만, 양자컴퓨팅 기술이 발전하면 인류가 직면한 많은 난제를 해결할 수 있을 거라고 믿어요. 앞으로 양자컴퓨팅 분야의 발전을 꾸준히 지켜보고 응원해야겠어요! 🤗
더 자세한 정보를 얻고 싶다면, 다음 자료들을 참고해보세요.
- Qiskit Textbook: https://qiskit.org/textbook/
- Cirq Documentation: https://quantumai.google/cirq
- 양자컴퓨팅 관련 논문 및 학회 자료
양자 게이트 종류, 더 깊이 알아볼까요? 🧐
양자 게이트 종류에 대한 기본적인 내용을 살펴보았으니, 조금 더 심화된 내용을 알아볼까요? 양자 게이트는 단순히 큐비트를 조작하는 도구일 뿐만 아니라, 양자 알고리즘의 성능을 결정하는 중요한 요소이기도 해요. 💡
양자 게이트의 충실도 (Fidelity) 측정 🎯

실제 양자 컴퓨터에서는 양자 게이트가 완벽하게 작동하지 않을 수 있어요. 😭 양자 게이트의 성능을 평가하는 지표 중 하나가 ‘충실도 (Fidelity)’인데요, 충실도는 양자 게이트가 얼마나 이상적으로 작동하는지를 나타내는 값이에요. 충실도가 높을수록 양자 게이트의 성능이 좋다고 할 수 있죠. 양자 게이트의 충실도를 높이기 위한 연구가 활발하게 진행되고 있답니다.
양자 게이트의 보편성 (Universality) ♾️
몇몇 양자 게이트들을 조합하면 임의의 양자 연산을 근사적으로 구현할 수 있다는 사실을 알고 계셨나요? 이러한 성질을 ‘보편성 (Universality)’이라고 해요. 즉, 보편적인 양자 게이트 세트만 있으면 모든 양자 알고리즘을 구현할 수 있다는 뜻이죠! CNOT 게이트와 단일 큐비트 게이트 (Hadamard, Pauli 등)는 대표적인 보편적인 양자 게이트 세트랍니다.
양자 게이트와 양자 회로 최적화 ⚙️
양자 회로를 설계할 때 어떤 양자 게이트를 사용할지, 어떤 순서로 배치할지에 따라 회로의 복잡도와 성능이 달라질 수 있어요. 따라서 양자 회로를 최적화하는 것은 매우 중요한 과제랍니다. 양자 회로 최적화 기술은 양자 알고리즘의 효율성을 높이고 양자 컴퓨터의 자원을 효율적으로 사용하는 데 기여할 수 있어요.
위상 게이트 (Phase Gate): 큐비트의 위상을 조절 🎛️
Pauli-Z 게이트처럼 큐비트의 위상을 조절하는 게이트를 위상 게이트라고 해요. 위상 게이트는 양자 알고리즘에서 양자 간섭을 일으키거나 특정 상태를 선택적으로 증폭하는 데 사용돼요. 대표적인 위상 게이트로는 S 게이트와 T 게이트가 있답니다.
- S 게이트: 큐비트의 |1⟩ 상태에 위상 인자 i를 곱해요.
- T 게이트: 큐비트의 |1⟩ 상태에 위상 인자 exp(iπ/4)를 곱해요.
Toffoli 게이트: 양자 AND 게이트 🚦
Toffoli 게이트는 세 개의 큐비트를 사용하는 게이트로, 두 개의 제어 큐비트가 모두 1이면 대상 큐비트의 상태를 반전시켜요. Toffoli 게이트는 양자 AND 게이트라고도 불리며, 양자 회로에서 비선형 연산을 구현하는 데 사용돼요. Toffoli 게이트는 양자 컴퓨팅의 보편성을 증명하는 데 중요한 역할을 했답니다.
양자 게이트 종류 글을 마치며… 📝
양자 게이트 종류에 대한 긴 여정을 함께 해주셔서 정말 감사해요! 😊 양자컴퓨팅은 아직 연구 단계에 있지만, 미래 사회에 큰 영향을 미칠 가능성이 높은 분야예요. 이번 글을 통해 여러분이 양자 게이트와 양자컴퓨팅에 대한 기본적인 이해를 얻고, 더 나아가 양자 분야에 관심을 갖게 되셨기를 바랍니다. 🙌
양자컴퓨팅은 어렵지만, 꾸준히 공부하고 관심을 가지면 누구나 이해할 수 있는 분야라고 생각해요. 앞으로도 양자컴퓨팅 관련 정보를 쉽고 재미있게 전달할 수 있도록 노력할게요. 궁금한 점이나 의견이 있다면 언제든지 댓글로 남겨주세요! 💬 함께 양자컴퓨팅의 미래를 만들어나가요! 🚀
양자 게이트 종류 관련 동영상







양자 게이트 종류 관련 상품검색



