양자 컴퓨터, 그 속도를 넘어! 그로버 알고리즘 활용법 🚀

혹시, 아직도 ‘양자 컴퓨터’ 하면 너무 어렵고 먼 미래 이야기 같나요? 😥 아니에요! 그 놀라운 잠재력, 특히 그로버 알고리즘은 우리 바로 곁에 성큼 다가와 있다는 사실! 이 글을 놓치면 엄청난 기회를 놓치는 걸지도 몰라요! 😉

이 글 하나로 끝! 그로버 알고리즘 활용법 핵심 정리:

🔎 시간 복잡도 완전 분석: 그로버 알고리즘, 얼마나 빠른지 속 시원하게 알려드릴게요!
🚀 최적화 전략 대방출: 검색 속도, 한계까지 끌어올리는 비법 공개!
💡 미래 응용 가능성: 그로버 알고리즘, 어디까지 활용될 수 있을까?

Table of Contents

그로버 알고리즘, 대체 뭔데? 🤔

양자 컴퓨터의 핵심 알고리즘 중 하나인 그로버 알고리즘! 🔍 쉽게 말해, 데이터베이스 검색 속도를 엄청나게 빠르게 만들어주는 마법 같은 존재랍니다. ✨ 기존 컴퓨터로는 상상도 못 할 속도로 말이죠! 마치 엄청나게 큰 도서관에서 원하는 책을 눈 깜짝할 사이에 찾아내는 것과 같아요. 📚

👉 '그로버 알고리즘 활용' 바로가기

왜 그로버 알고리즘에 주목해야 할까? ✨

단순히 ‘빠르다’는 말로는 설명이 부족해요! 😲 그로버 알고리즘은 기존 알고리즘으로는 해결하기 어려웠던 문제들을 해결할 수 있는 가능성을 열어준답니다. 예를 들어, 신약 개발 🧪, 금융 시장 분석 📈, 인공지능 🤖 등 다양한 분야에서 혁신을 가져올 수 있어요. 미래 사회의 게임 체인저가 될 거라는 사실! 😎

그로버 알고리즘 시간 복잡도, 파헤쳐 보자! 🤯

본격적으로 시간 복잡도 이야기를 해볼까요? 😅 너무 어렵게 생각하지 마세요! 쉽게 설명해 드릴게요.

👉 '그로버 알고리즘 활용' 바로가기

Big O 표기법, 알고리즘 효율성의 척도 📏

알고리즘의 효율성을 나타내는 방법 중 하나인 Big O 표기법! 척도라고 생각하면 쉬운데요. 간단하게 말해, 입력 데이터의 크기가 커질수록 알고리즘의 실행 시간이 얼마나 늘어나는지를 나타내는 방법이에요. ⏱️ 예를 들어, O(n)은 데이터가 2배로 늘면 실행 시간도 2배로 늘어난다는 의미고, O(log n)은 데이터가 2배로 늘어도 실행 시간은 조금밖에 늘어나지 않는다는 뜻이죠.

그로버 알고리즘, 얼마나 빠를까? 🚀

그로버 알고리즘의 시간 복잡도는 O(√N) 이에요. 여기서 N은 데이터베이스의 크기를 의미하죠. 🤔 이게 무슨 뜻이냐고요? 기존 알고리즘인 선형 탐색(Linear Search)의 시간 복잡도가 O(N)인 것에 비하면 엄청나게 빠른 속도라는 거죠! 💨 예를 들어, 100만 개의 데이터 중에서 원하는 정보를 찾는다고 가정해 볼게요. 선형 탐색은 평균적으로 50만 번을 시도해야 하지만, 그로버 알고리즘은 단 1,000번 만에 찾을 수 있다는 놀라운 사실! 🤩

알고리즘	시간 복잡도	설명
선형 탐색	O(N)	데이터베이스의 모든 요소를 하나씩 비교하며 탐색
그로버 알고리즘	O(√N)	양자 중첩과 간섭을 이용하여 데이터베이스를 더 빠르게 탐색

👉 위키백과 '그로버 알고리즘 활용' 검색

수학적 증명, 너무 깊게 들어가지 말자! 🙅‍♀️

물론, 그로버 알고리즘의 시간 복잡도를 완벽하게 이해하려면 선형 대수와 양자 역학에 대한 깊은 지식이 필요해요. 😥 하지만 너무 걱정하지 마세요! 이 글에서는 핵심 개념만 짚고 넘어갈 거예요. 😇 중요한 건, 그로버 알고리즘이 기존 알고리즘보다 훨씬 빠르다는 사실을 이해하는 거니까요! 😉

그로버 알고리즘, 검색 속도 향상 전략 🚀

그렇다면, 그로버 알고리즘을 어떻게 활용해야 검색 속도를 최대한으로 끌어올릴 수 있을까요? 몇 가지 핵심 전략을 소개해 드릴게요!

앰플리튜드 증폭 기술, 확률을 높여라! 🍀

👉 나무위키 '그로버 알고리즘 활용' 검색

그로버 알고리즘의 핵심은 바로 앰플리튜드 증폭(Amplitude Amplification) 기술이에요. 🍀 쉽게 말해, 원하는 답이 나올 확률을 점점 높여주는 기술이죠. 양자 중첩과 간섭을 이용해서 말이에요! 마치 로또 당첨 확률을 높이는 비법과 같다고 할까요? 😜

최적의 반복 횟수, 효율성을 극대화! 📈

그로버 알고리즘을 무작정 반복한다고 해서 항상 좋은 결과가 나오는 건 아니에요. 🙅‍♀️ 최적의 반복 횟수를 찾는 것이 중요하답니다. 반복 횟수가 너무 적으면 원하는 답을 찾지 못할 확률이 높아지고, 너무 많으면 오히려 효율성이 떨어질 수 있어요. 마치 운동할 때 적절한 세트 수와 반복 횟수를 정하는 것과 비슷하죠! 💪

👉 지식백과 '그로버 알고리즘 활용' 검색

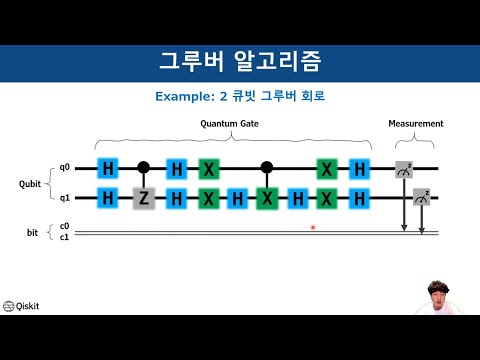
양자 회로 최적화, 성능을 끌어올려라! ⚙️

그로버 알고리즘은 양자 회로(Quantum Circuit)를 통해 구현되는데요. 이 양자 회로를 어떻게 설계하느냐에 따라 성능이 크게 달라질 수 있어요. ⚙️ 최적화된 양자 회로를 설계하면 그로버 알고리즘의 성능을 극대화할 수 있답니다. 마치 자동차 엔진을 튜닝하는 것과 같다고 할까요? 🏎️

양자 어닐링과의 비교, 뭐가 다를까? 🤔

양자 컴퓨팅 분야에는 그로버 알고리즘 외에도 양자 어닐링(Quantum Annealing)이라는 또 다른 방식이 존재해요. 🤔 두 방식은 문제 해결 방식에서 큰 차이를 보인답니다.

특징	그로버 알고리즘	양자 어닐링
문제 유형	구조화되지 않은 데이터베이스 검색	최적화 문제
작동 방식	앰플리튜드 증폭을 이용한 확률적 탐색	양자 터널링을 이용한 최적 해 탐색
장점	특정 문제에서 매우 빠른 속도 제공	다양한 최적화 문제에 적용 가능
단점	양자 회로 구현의 어려움, 특정 문제에만 적용 가능	그로버 알고리즘에 비해 속도가 느릴 수 있음

그로버 알고리즘, 미래는 밝을까? ✨

양자 컴퓨터 기술이 발전함에 따라 그로버 알고리즘의 활용 가능성은 더욱 무궁무진해질 것으로 예상돼요. 🤩 특히, 데이터 규모가 크고 복잡한 문제에서 그 진가를 발휘할 것으로 기대됩니다. 👍

그로버 알고리즘, 이렇게 활용해 보세요! 🚀

신약 개발: 방대한 분자 데이터베이스에서 특정 효능을 가진 물질을 빠르게 검색! 🧪
금융 시장 분석: 복잡한 금융 데이터에서 이상 징후를 신속하게 탐지! 📈
인공지능: 머신러닝 모델 학습 속도를 획기적으로 향상! 🤖
암호 해독: (물론 윤리적인 문제도 고려해야 하지만) 암호 해독 속도를 높여 보안 취약점 분석! 🔐
물류 최적화: 복잡한 물류 네트워크에서 최적의 경로를 빠르게 탐색! 🚚

그로버 알고리즘 활용, 콘텐츠 연장 🚀

양자 얽힘과 그로버 알고리즘의 관계 🔗

양자 얽힘(Quantum Entanglement)은 두 개 이상의 양자가 서로 연결되어 마치 하나의 시스템처럼 행동하는 현상을 말해요. 🔗 이러한 얽힘 상태는 그로버 알고리즘의 정보 처리 및 계산 속도를 향상시키는 데 중요한 역할을 한답니다. 😮

양자 간섭과 그로버 알고리즘의 핵심 원리 🌈

양자 간섭(Quantum Interference)은 양자 세계에서 파동의 중첩으로 인해 특정 상태가 강화되거나 상쇄되는 현상을 말해요. 🌈 그로버 알고리즘은 이러한 양자 간섭을 이용하여 원하는 답에 해당하는 앰플리튜드를 증폭시키고, 그렇지 않은 답은 상쇄시켜 검색 속도를 높인답니다. ✨

그로버 알고리즘의 한계점과 극복 방안 🚧

그로버 알고리즘은 분명 획기적인 알고리즘이지만, 아직 해결해야 할 과제들이 남아있어요. 🚧 예를 들어, 양자 컴퓨터의 안정성 문제, 양자 회로 구현의 어려움 등이 있죠. 이러한 한계점을 극복하기 위해 양자 오류 수정 기술, 양자 알고리즘 최적화 연구 등이 활발하게 진행되고 있답니다. 🔬

그로버 알고리즘과 다른 양자 알고리즘과의 비교분석 ⚔️

그로버 알고리즘 외에도 쇼어 알고리즘(Shor’s Algorithm), 양자 푸리에 변환(Quantum Fourier Transform) 등 다양한 양자 알고리즘이 존재해요. ⚔️ 각 알고리즘은 특정 문제에 특화되어 있으며, 서로 보완적인 관계를 가지고 있답니다. 예를 들어, 쇼어 알고리즘은 큰 수의 소인수 분해에 특화되어 있고, 그로버 알고리즘은 데이터베이스 검색에 특화되어 있죠.